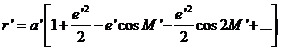9.3
Movimiento orbital de la Luna
El estudio del movimiento de la Luna es uno de los problemas más difíciles de la Mecánica Celeste debido a que es el cuerpo perturbador y no el astro central el que posee la masa preponderante, lo cual hace que la órbita que describe la Luna alrededor de la Tierra se separe mucho de una órbita kepleriana y, en consecuencia, la teoría de la Luna deba de construirse de distinta manera a la que explica el movimiento de los planetas.
Ya desde la antigüedad se habían ido descubriendo empíricamente ciertas desigualdades tales como la ecuación del centro, utilizada por Hiparco; la evección, introducida por Tolomeo; la variación, corrección introducida por Tycho Brahe, y la ecuación anual. Pero, era imposible detectar de la misma manera un gran número de otras desigualdades no despreciables, aunque menos importantes, que se superponían a las desigualdades principales, las cuales se pusieron de manifiesto al estudiar la teoría del movimiento de la Luna analíticamente.
Newton se ocupó del estudio de las grandes desigualdades llegando hasta una segunda aproximación. A partir de Newton la teoría de la Luna ha sido ampliamente desarrollada, habiéndose empleado desde entonces métodos que difieren considerablemente unos de otros y que presentan sus ventajas o inconvenientes en determinados aspectos.
Se suelen distinguir tres tipos de teorías: analíticas,
analítico-numéricas y numéricas. Entre las primeras podemos destacar la de
Delaunay, que desarrolló completamente la función perturbatriz hasta cantidades
de séptimo orden. Las analítico-numéricas empiezan con la de Laplace que
mantiene las dos excentricidades y el 
como parámetros y atribuye
un valor numérico a 
. Pertenece a esta clase la teoría de Hill-Brown. Airy
propuso una aproximación puramente numérica al problema de mejorar la teoría de
Delaunay, pero sin éxito. Recientemente Eckert ha aplicado la técnica de Airy a
la teoría de Brown del problema lunar principal, es decir, el de hallar el
movimiento de la Luna bajo la acción gravitatoria de la Tierra y del Sol
considerando los tres cuerpos como masas puntuales, y por otra parte, Deprit ha
confeccionado analíticamente unas efemérides lunares que mejoran dicha teoría
de Brown.
La Luna se mueve alrededor de la Tierra en una órbita aproximadamente elíptica cuyos valores medios del semieje mayor, la excentricidad y la inclinación son
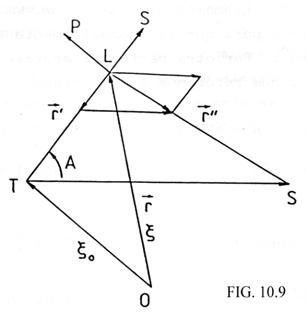
Ya hemos dicho que el movimiento de la Luna es fuertemente perturbado
por el Sol. Por esta causa estos tres elementos están sujetos a variaciones
periódicas alrededor de dichos valores. La excentricidad varía de 0.044 a
0.067, la inclinación oscila entre 4º 58
y 5º 19, y el eje mayor gira en sentido directo con un periodo de 8 años 310
días.
Podemos definir varios periodos de revolución de la Luna en su órbita. Llamamos revolución sinódica al intervalo medio de dos conjunciones sucesivas de la Luna y del Sol (lunas nuevas). Se calcula su duración a partir del conocimiento de épocas en que se han producido eclipses de Sol separadas por intervalos de tiempo muy largos. Su es de 29.5305883 días = 29d 12h 44m 2s.8. Es la lunación que regula las fases de la Luna y los eclipses. Constituye el mes de los antiguos calendarios lunares.
Revolución sidérea es el tiempo necesario para que la longitud media de la Luna referida a un equinoccio fijo aumente 360º . Su valor es de 27.32166150 días =27d 7h 43m 11s.5. Durante un mes sidéreo el Sol ha recorrido aproximadamente 1/12 de su órbita y, por consiguiente, al cabo de una revolución sidérea la Luna no presentará la misma fase.
El movimiento medio sinódico
de la Luna es la diferencia entre el movimiento
medio sidéreo nde la Luna y el movimiento medio sidéreo n del Sol y vale:
De aquí que, siendo
n = 3548.1928,
Si dividimos 
por este valor de n
encontraremos el número de días de una revolución sidérea.
Revolución trópica es el tiempo necesario para que la ascensión recta media de la Luna
aumente en 24 horas. Su valor se halla dividiendo 1296000
por el del movimiento medio
trópico de la Luna, referido al equinoccio medio móvil, que se obtiene
sumando la precesión diurna 
al movimiento medio
sidéreo. Es decir,
Hemos dicho que el periodo de revolución del eje mayor de la órbita de
la Luna es de 8 años 310 días. Dividiendo 1296000 por dicha cantidad hallaremos el valor del movimiento sidéreo medio del perigeo m = 400.9167. Llamamos revolución
anomalística al tiempo necesario para que la anomalía media de la Luna
aumente en 360º. Por otra parte, el movimiento
medio anomalístico, que referimos a su perigeo móvil, valdrá:
y por tanto, la duración de una revolución anomalística será de
También hemos dicho que la inclinación del plano de la órbita de la
Luna sobre la eclíptica sufre variaciones periódicas. De ellas, la más
importante tiene una semiamplitud de 9 y un periodo de 173 días. Asimismo, la línea de los nodos retrograda
secularmente, siendo el valor del movimiento medio sidéreo de
n = -3 10.77 y el periodo de revolución correspondiente de 18.60 años (ver 8.7).
Se llama revolución draconítica al intervalo medio de dos pasos consecutivos de la Luna por el nodo ascendente de su órbita. La duración de una revolución draconítica es:
Este periodo rige las variaciones de la latitud celeste de la Luna y juega un papel importante en la predicción de eclipses.
9.3.2 Desarrollo de la fuerza perturbatriz
En la exposición de este apartado seguimos a Danjon
cuyo desarrollo de la teoría de la Luna lleva a una primera aproximación de la
teoría de Delaunay.
Supondremos, de momento, que la inclinación i de la órbita lunar es nula y que, por consiguiente, la fuerza
perturbatriz está situada en su plano (i2 = 0.008).
Tomaremos la masa del Sol como unidad y llamaremos m y m a las masas de la Tierra y de la Luna, respectivamente, e y ea las excentricidades de sus órbitas, a y a sus semiejes mayores, n y na sus movimientos medios y r
y ra los radios vectores geocéntricos del Sol y de la Luna (Fig.
10.9). Los símbolos 
y L representarán las longitudes geocéntricas del Sol y de la Luna. Las
latitudes se supondrán nulas. Sean S,
T y L los centros del Sol, la Tierra y la Luna respectivamente (Fig. 10.9); hagamos
Sean, por otra parte, O el
origen de un sistema inercial de referencia y 
y 
los vectores de posición
de la Tierra y de la Luna en dicho sistema. El movimiento de T vendrá definido por
(55.9)
y el de L por
(56.9)
Restando estas dos igualdades miembro a miembro tendremos
(57.9)
que representa el movimiento de la Luna alrededor de la Tierra. El segundo término del segundo miembro es la fuerza perturbatriz debida a la atracción solar (recordar (44.7) de 7.5).
Hagamos G M=k y
descompongamos 
en suma de dos
vectores, uno dirigido de L hacia T y el paralelo a TS. Tendremos:
(58.9)
con lo que la expresión de la fuerza perturbatriz será ahora
(59.9)
(60.9)
Las componentes S y P de 
según el radio vector
y según la normal al radio vector son:
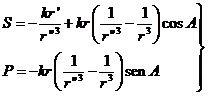(61.9)
De la misma figura 10.9 se deduce:
de donde:
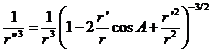
Desarrollando y limitando al segundo orden con relación a r/r, obtenemos:
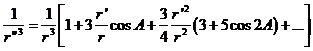(62.9)
y llevando este valor a las expresiones (61.9) de S y P, haciendo k = n2a3, lo cual supone despreciar las masas de la Luna y de la Tierra frente a la del Sol, obtenemos finalmente:
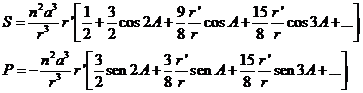(63.9)
Más adelante se introducirán en estas expresiones los elementos keplerianos; pero, hemos de observar que los elementos keplerianos del Sol se refieren, no al centro de la Tierra, sino al baricentro del sistema Tierra-Luna.
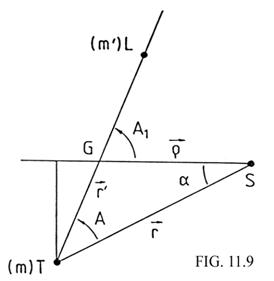
Sea 
el radio vector de
dicho baricentro y A1 el
ángulo que forma con TL (Fig. 11.9). Tendremos:
o sea:
Luego, teniendo en cuenta que G T es muy pequeño, podemos escribir con mucha aproximación:
y
De (64.9) deducimos:
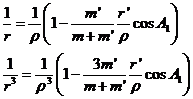
valores que sustituidos juntamente con (65.9) en (63.9) nos dan
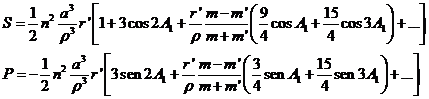(66.9)
Vamos a introducir ahora los elementos keplerianos utilizando, para representar los radios vectores, los desarrollos (48.3) y (49.3), que escritos para nuestro caso nos dan:
(67.9)
donde e y M son la excentricidad y anomalía media del baricentro y e’ y M’ son la excentricidad y anomalía media de la Luna.
El ángulo A1, diferencia entre la longitud de la Luna y la longitud baricéntrica del Sol, puede expresarse en función de los movimientos medios sidéreos n y n’ del Sol y de la Luna y de las desigualdades keplerianas periódicas de las longitudes de estos astros que designaremos respectivamente por SP y SP’.
Pondremos
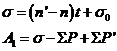(69.9)
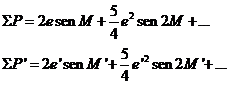(70.9)
En el desarrollo de la fuerza perturbatriz intervienen términos en senjA1 y cosjA1 donde j es un entero. Teniendo en cuenta el valor de (69.9) de A1 podemos escribir:
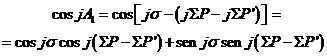
y desarollando en serie:
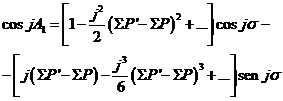(71.9)
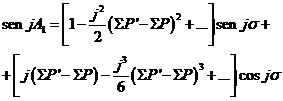(72.9)
Es fácil ver que sustituyendo (70.9) en (71.9) y (72.9) obtendremos en las
expresiones de cosjA1 y
senjA1 productos de senos
de los ángulos M, M, 2M, 2M, etc. afectados de exponentes enteros. Estos productos se podrán
transformar en sumas de senos y cosenos, que multiplicadas por senjs y cosjs nos proporcionarán cosjA1 y senjA1 bajo la forma de sumas de cosenos o de senos con
argumentos combinaciones lineales de los ángulos s, M y M.
Total, que sustituyendo (67.9), (68.9)
y los valores hallados para cosjA1
y senjA1 en (66.9), obtendremos unas nuevas expresiones de S y P
en las que aparecerán e, e, a, a, s , M, M y múltiplos de los argumentos s, M y M. Pero, los desarrollos de S
y P no se utilizan para estudiar las
perturbaciones que dependen de e; en consecuencia, cuando interese, despreciaremos los términos en que
aparezca e y escribiremos solamente los que dependan de e.
Teniendo en cuenta todo lo expuesto queda, finalmente.
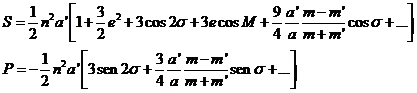(73.9)
desarrollo que
utilizaremos, como queda dicho, para el estudio de perturbaciones que no
dependen de e.
9.3.3 Desarrollo de la
función perturbatriz
Cuando interese estudiar las perturbaciones que dependen de la excentricidad e’ utilizaremos la función perturbatriz (recordar (74.8))
(74.9)
De la Fig. 10.9 deducimos:
y
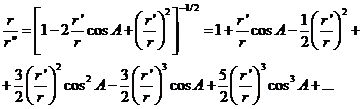
Sustituyendo en (74.9) obtenemos el siguiente desarrollo de la función perturbatriz:
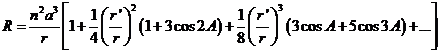
en el que los primeros términos despreciados son los de cuarto orden en r’/r . Si se omite el primer término, el cual no contiene los elementos de la órbita lunar y por consiguiente no intervendrá en las derivadas parciales, queda:
(75.9)
Podemos expresar R en función
de e, e, a, a, s, M, My múltiplos de los argumentos s, M y M, añadiendo a los desarrollos parciales que hemos utilizado para
obtener S y P
Obtendremos:
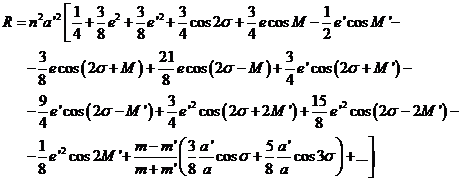(76.9)
Si tuviéramos en cuenta la inclinación i , a los argumentos que figuran en el desarrollo (76.9)
deberíamos añadir la distancia de la Luna a su nodo ascendente, 
.
9.3.4 Perturbaciones independientes de la excentricidad
de la órbita lunar
Para estudiar las perturbaciones independientes de la excentricidad ede la órbita de la Luna utilizaremos las ecuaciones del movimiento en
la forma
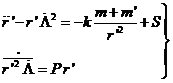(77.9)
que se deduce de las ecuaciones del movimiento en coordenadas polares
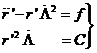
donde f representa el módulo de la fuerza
central ejercida sobre la unidad de masa y C
es la constante de las áreas, recordando además que si u y w son las componentes
de la velocidad orbital el efecto de la fuerza perturbatriz durante el tiempo dt se puede representar por du = Sdt , dw = Pdt y de esta segunda se deduce rdw = dC = rPdt.
La primera de las ecuaciones (77.9) expresa la aceleración radial en coordenadas polares y la segunda, la aceleración normal al radio vector.
La integración de estas ecuaciones con un grado de aproximación suficiente para establecer las Tablas de la Luna es una operación muy complicada. Sin embargo, se pueden establecer algunas reglas conducentes a la simplificación del problema:
1ª) Introduciremos sucesivamente, en las ecuaciones del movimiento, cada uno de los términos de la fuerza perturbatriz y estableceremos la perturbación correspondiente como si existiera sola.
2ª) Integraremos
las ecuaciones como si los argumentos s, M y M fueran funciones lineales del tiempo y, por consiguiente, despreciando
en los segundos miembros las perturbaciones de las cuales son afectados.
3ª) Cuando en los segundos miembros aparezcan a la vez términos de largo periodo y términos de corto periodo despreciaremos estos últimos.
Los resultados que se obtienen observando estas reglas constituyen la llamada segunda aproximación de la teoria de la Luna.
a) Término constante de la fuerza perturbatriz:
En (73.9) P no contiene término constante; por consiguiente, el segundo miembro de la segunda ecuación de (77.9) es nulo y el movimiento obedece a la ley de las areas. Por otra parte, la primera ecuación de (77.9) se puede escribir, teniendo en cuenta el desarrollo de S:
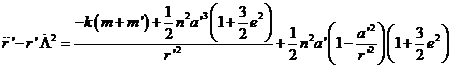
y puesto que
estamos suponiendo e = 0, será a= r (órbita circular) y por tanto el segundo sumando del segundo miembro
será cero. La ecuación resultante, junto con la que expresa la ley de las
áreas, determina un movimiento circular que se escribe
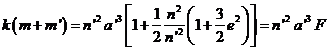(78.9)
donde F = 1.0028. Una teoría más completa
teniendo en cuenta e e i da para F el valor
El efecto de este factor es una reducción de la atracción de la Tierra sobre la Luna causada por la presencia del Sol.
b) Variación: Es una desigualdad del movimiento
de la Luna, descubierta por Tycho Brahe en 1582 y de la cual Newton dio la
teoría en su obra “Principios Matemáticos de la Filosofía Natural y su Sistema
del Mundo”. Su periodo es de una semi-revolución sinódica; se anula en las
sicigias y en las cuadraturas y toma su valor máximo en los octantes donde
sobrepasa los 39. Estas circunstancias bastan para saber que el argumento del cual
depende es el doble del ángulo s definido como la diferencia entre las longitudes medias de la Luna y
del Sol:
(79.9)
Para calcularla partamos de las ecuaciones (77.9), sustituyamos en ellas los valores
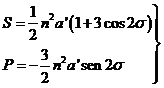(80.9)
deducidos de (73.9) y tengamos en cuenta los resultados obtenidos en el párrafo a). Escribiremos:
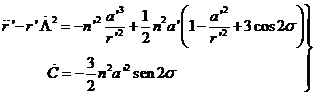(81.9)
Integremos
suponiendo constantes n y a: La segunda da, por integración inmediata
de donde, siendo el
valor medio de C na2 es
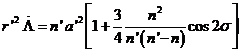(82.9)
Despejando de (82.9) 
, elevando al cuadrado, desarrollando en serie y despreciando
los términos en 4s , hallamos
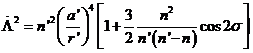(83.9)
valor que sustituido en la primera de las ecuaciones (81.9) nos proporciona
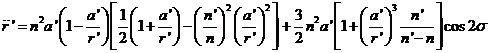
y si, puesto que 
reemplazamos 
por 1 en las dos expresiones
entre corchetes, resulta:
Busquemos una solución de (84.9) de la forma
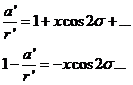(85.9)
(86.9)
Sustituyendo (85.9) y (86.9) en (84.9) resulta
(87.9)
(recordar
que n = 3548
.l928
y n= 47434.8907).
Este resultado nos dice que la Luna describe un óvalo cuyo semieje
menor, r= a (1-x), está dirigido hacia
el Sol (s = 0). La razón de sus ejes es:
Como consecuencia, la paralaje de la Luna es más pequeña en las cuadraturas que en las sicigias en aproximadamente 1/60.
Consideremos de nuevo la ecuación (82.9) y sustituyamos en ella
Tendremos, despreciando términos de orden superior
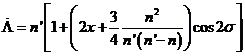
e integrando:
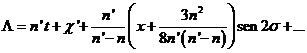(88.9)
La desigualdad que aparece en la expresión (87.9) de la longitud de la Luna es la variación. Su coeficiente, calculado a partir de esta fórmula es
0.01022 = 35
.1.
Si desarrollamos en serie el valor de x dado por (87.9) obtenemos
resultando para el coeficiente de la variación la serie
cuyos dos primeros términos constituyen los de una serie lentamente convergente que estableció Delaunay de la forma:
(89.9)
cuya suma es:
Si se tuvieran en cuenta los términos que dependen de las
excentricidades y de la inclinación, la variación llegaría a valer 39 30
c) Desigualdad paraláctica: es una desigualdad del movimiento de la Luna que depende del argumento s y cuyo periodo es igual a la revolución sinódica.
Los términos correspondientes de la fuerza perturbatriz son:
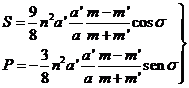(90.9)
que sustituiremos
en las ecuaciones (77.9) tomando el cociente 
. Teniendo en cuenta, además, (78.9)
obtendremos:
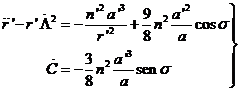(91.9)
La segunda ecuación se integra inmediatamente, resultando:
de donde tomando 
es:
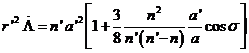(92.9)
Eliminando entre esta ecuación y
la primera de las (91.9) obtenemos
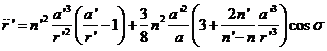(93.9)
o, también,
haciendo como antes r = asalvo en el factor 
:
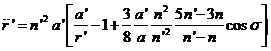(94.9)
Busquemos una solución de la forma
(95.9)
Será
y
Sustituyendo en (94.9) y operando obtendremos:
de donde
x = 0.0752
A partir de (96.9) podemos desarrollar x en términos de n/n:
pero, una teoría más completa nos diría que sólo el primer término de este desarrollo es exacto.
Calculemos la desigualdad correspondiente de la longitud. De (92.9) teniendo en cuenta (95.9), se deduce
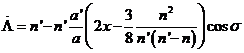
e integrando:
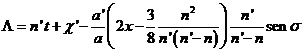
y teniendo en cuenta el desarrollo de x:
(97.9)
En la teoría de Delaunay el coeficiente de la desigualdad paraláctica se desarrolla de la siguiente forma:
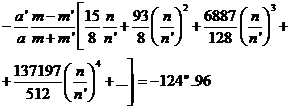(98.9)
El efecto de los términos (90.9) de la fuerza perturbatriz sobre la órbita de la Luna es una deformación sobre la misma en el sentido de que el radio de curvatura de la trayectoria perturbada es mayor en la luna nueva que en la llena y la órbita, por tanto, no es centrada, estando su centro desplazado hacia el Sol.
Debido a la deformación de la órbita, la paralaje de la Luna disminuye
en 1 cerca de la luna nueva y aumenta de la misma cantidad en la
luna llena. La variación correspondiente de la distancia a la Tierra es, en media,
de ±110 km.
La observación de ocultaciones de estrellas por la Luna proporciona el valor del coeficiente (98.9) con mucha precisión, ya que la desigualdad paraláctica retrasa las ocultaciones en 3m 48s en cuarto creciente y las avanza otro tanto en cuarto menguante.
d) Ecuación anual: Es una variación periódica del movimiento medio de la Luna de periodo anual. Está ligada a la variación de la fuerza perturbatriz del Sol, que depende de l/r3 y de M. Fue descubierta, como la variación, por Tycho Brahe.
En (73.9) el desarrollo de S contiene un término en M y el desarrollo de P no lo contiene. La constante de las áreas puede por tanto considerarse aquí como invariable y las ecuaciones del movimiento (77.9) pueden escribirse en la forma:
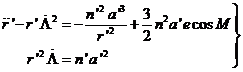(99.9)
Eliminemos entre estas dos
ecuaciones:
(100.9)
Busquemos una solución de la forma
de donde
y
Hagamos como siempre 
fuera del paréntesis
en (100.9). Tendremos:
o tambien:
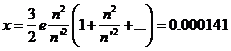(102.9)
Sustituyendo en la segunda de (99.9) el valor de 
dado por (101.9), obtenemos
e integrando:
(103.9)
El coeficiente 
de esta desigualdad es
de unos -12.5 y su desarrollo
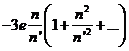(104.9)
tiene por primer
término 
; no contiene término en 
y el término en 
no puede deducirse de
la teoría que estamos desarrollando.
Delaunay obtiene el siguiente desarrollo del coeficiente de la ecuación anual:
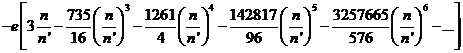
cuya suma es -11 2.
Si se añadiesen los términos que dependen de la excentricidad e, su valor sería de -118.
Debido a la ecuación anual, del 2 de enero al 2 de julio la Luna está retrasada sobre la Luna media y esta avanzada del 2 de julio al 2 de enero siguiente. A principios de abril los eclipses y las ocultaciones se retrasan en más de 20 minutos y se adelantan en la misma cantidad a principios de octubre.
a) Aceleración secular: En 1787 Laplace demostró que la variación secular de la excentricidad e de la órbita de la Tierra tiene como consecuencia una aceleración secular del movimiento medio de la Luna. En efecto, la distancia media del Sol a la Tierra tiene por expresión
(105.9)
variando, por
tanto, en el mismo sentido que la excentricidad; por consiguiente, la fuerza
perturbatriz, no periódica, ejercida por el Sol sobre la Luna, varía también
secularmente, dando lugar al fenómeno, que había sido observado ya por Halley
en 1693, por el cual el movimiento medio de la Luna obtenido comparando
observaciones de eclipses reseñados por Tolomeo (siglo II) y de eclipses
observados por los árabes (siglo IX) era menor que el que se deducía de
comparar estos últimos con las observaciones de eclipses contemporáneos.
Lalande fijó en 10 por siglo el valor de esta variación, dándole el nombre de aceleración secular de la Luna.
Hemos dicho en el apartado a) que el valor k(m + m) dado por (78.9) es
constante. Ahora bien, en el segundo miembro de dicha expresión figura la
excentricidad e que decrece
secularmente; por tanto, los elementos de la órbita lunar n y a han de ser variables. Por otra parte, la expresión de la
componente P de la fuerza
perturbatriz (recordar 73.9) no contiene más que términos
periódicos, y en consecuencia, la constante de las áreas
es también invariante.
Eliminando a’ entre (106.9) y (78.9) se deduce
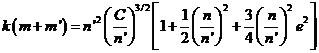
y teniendo en cuenta que
es invariante, tendremos:
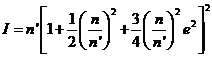(107.9)
siendo I una constante.
De (107.9) se deduce fácilmente la derivada del
movimiento medio n con relación a la excentricidad e:
(108.9)
Tomemos
entonces,
de donde, tomando sólo el término en h:
e integrando
y
(109.9)
Tomando en el coeficiente de t2 los valores de e0 y h de la teoría de Newcomb, se deduce para la aceleración secular:
estando el tiempo t expresado en siglos.
El desarrollo del término b dado por Delaunay es
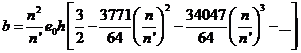(110.9)
siendo b
= 6.
Hoy en día se evalua en 12.36 el valor de b
exigido por las observaciones.
En realidad, la aceleración secular de la Luna es una desigualdad periódica de periodo muy largo ya que actualmente la excentricidad de la órbita de la Tierra está decreciendo y lo continuará haciendo durante 24.000 años aproximadamente; pasará entonces a crecer y la variación correspondiente del movimiento medio de la Luna cambiará de sentido.
Siendo invariante el producto n2 a3, y
conocido el aumento secular del movimiento medio n, se deduce la disminución correspondiente de la distancia a, resultando ser de menos de 2m por siglo.