9.3.5 Perturbaciones que dependen de la excentricidad de la
órbita
lunar
Para estudiar las variaciones que dependen de la excentricidad e![]() de la órbita de la Luna utilizaremos, como indicamos en 9.3.3, la función perturbatriz R que sustituiremos en las ecuaciones de Gauss (119.8) adecuadas a nuestro caso. Supondremos nula la
inclinación de la órbita y despreciaremos los términos en el cuadrado de la
excentricidad, con lo que dichas ecuaciones tomarán la forma:
de la órbita de la Luna utilizaremos, como indicamos en 9.3.3, la función perturbatriz R que sustituiremos en las ecuaciones de Gauss (119.8) adecuadas a nuestro caso. Supondremos nula la
inclinación de la órbita y despreciaremos los términos en el cuadrado de la
excentricidad, con lo que dichas ecuaciones tomarán la forma:
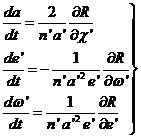 (111.9)
(111.9)
Los únicos términos de la función perturbatriz que intervienen en las
derivadas de e![]() y de w
y de w![]() son los que contienen uno u otro de estos dos elementos. Por
tanto, a partir de (76.9) escribiremos:
son los que contienen uno u otro de estos dos elementos. Por
tanto, a partir de (76.9) escribiremos:
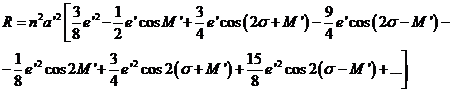 (112.9)
(112.9)
En el desarrollo que utilizaremos sólo consideraremos los términos no periódicos y los de periodo muy largo que son los que separan al máximo el cuerpo perturbado de su lugar medio.
El periodo de los términos en M![]() es próximo a un mes. El de los términos en 2s - M
es próximo a un mes. El de los términos en 2s - M![]() también es próximo a un mes ya que 2s -M
también es próximo a un mes ya que 2s -M![]() = 2(n
= 2(n![]() -n)t-n
-n)t-n![]() t = n
t = n![]() t-2nt y teniendo en cuenta que
t-2nt y teniendo en cuenta que ![]() /día y
/día y ![]() /día, la diferencia es de 11º/día ; por tanto 360º/11º
/día, la diferencia es de 11º/día ; por tanto 360º/11º![]() 32 días. El periodo de los términos en 2M
32 días. El periodo de los términos en 2M![]() es de
aproximadamente 14 días. Los de los términos en 2s + M
es de
aproximadamente 14 días. Los de los términos en 2s + M![]() y en 2(s + M) son respectivamente de unos 9 y 7 días.
Veamos cual es el del término 2(s - M
y en 2(s + M) son respectivamente de unos 9 y 7 días.
Veamos cual es el del término 2(s - M![]() ):
):
![]()
Si suponemos fijo el perigeo de la Luna, el periodo es de seis meses, o sea, mucho mayor que los otros.
Limitaremos, pues, la función perturbatriz a los siguientes términos:
Sustituyendo esta expresión de R en las ecuaciones (111.9) tendremos:
puesto que ![]() al no figurar en (113.9) la longitud de la Luna. Esto nos dice que el
semieje mayor no sufre perturbaciones que dependan del argumento
al no figurar en (113.9) la longitud de la Luna. Esto nos dice que el
semieje mayor no sufre perturbaciones que dependan del argumento
2(s -M![]() ).
).
a) Movimiento secular del perigeo: Para estudiar el movimiento del perigeo pongamos
![]()
y derivemos respecto al tiempo teniendo en cuenta (116.9):
![]() (117.9)
(117.9)
Integremos
efectuando el cambio de variable tanj = x y
haciendo ![]() ; tendremos:
; tendremos:
![]()
y sustituyendo en (117.9):
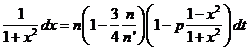
de donde:
![]()
e integrando
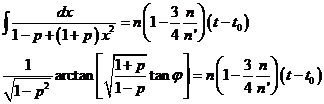
![]() (118.9)
(118.9)
Hagamos
![]()
Sustituyendo en (118.9) queda:
tanj = q tany
lo cual implica
![]() (119.9)
(119.9)
siendo el primer
término despreciado en sen 4y.
Podemos escribir, pues, la expresión que da la longitud del perigeo de la siguiente forma
![]()
o también:
![]()
y haciendo
![]()
sustituyendo el valor de p y agrupando los términos en t, queda finalmente:
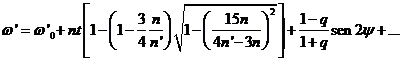 (120.9)
(120.9)
Vemos pues que el perigeo presenta un movimiento secular cuya velocidad angular media es
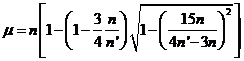
o, lo que es lo mismo:
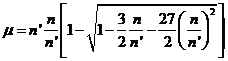 (121.9)
(121.9)
expresión
aproximada que da para el movimiento medio del perigeo el valor de 351![]() siendo el valor observado de 401
siendo el valor observado de 401![]() .
.
El desarrollo de (121.9) es
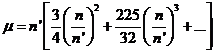
siendo la serie dada por Delaunay:
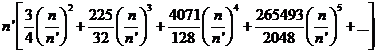
cuya suma es 400![]() .4688.
.4688.
Si se tienen en
cuenta otros términos que dependen de las excentricidades y de las
inclinaciones se halla m = 400![]() .9167 con un periodo de revolución de 8 años 310 días.
.9167 con un periodo de revolución de 8 años 310 días.
b) Movimiento
periódico del perigeo: La longitud del perigeo que acabamos de
obtener (120.9) contiene un término periódico cuyo
argumento y es la
parte secular del ángulo j (119.9). Si designamos por w![]() m la longitud media del perigeo y
despreciamos la excentricidad de la órbita terrestre, podemos escribir (120.9) de la forma:
m la longitud media del perigeo y
despreciamos la excentricidad de la órbita terrestre, podemos escribir (120.9) de la forma:
El coeficiente de la desigualdad es
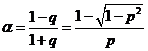 (123.9)
(123.9)
Sustituyendo p por su valor ![]() y desarrollando en
serie encontramos, en nuestro estudio, que sólo el primer término es válido
y desarrollando en
serie encontramos, en nuestro estudio, que sólo el primer término es válido
![]()
El valor de a es de 8º.7 y el periodo de la desigualdad es de 205.89 días.
c) Variaciones
de la excentricidad: Para poner en evidencia la desigualdad
correspondiente de la excentricidad partamos de las ecuaciones (115.9) y (116.9). Teniendo en cuenta
que estamos haciendo j = q - w![]() , podemos escribir
, podemos escribir
![]()
y, por tanto, sustituyendo en (116.9):
![]()
![]() (124.9)
(124.9)
y dividiendo (115.9) por (124.9) se obtiene
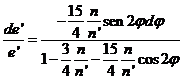 (125.9)
(125.9)
ecuación diferencial a variables separables que se integra inmediatamente, teniendo en cuenta que, a menos de un factor -2 el numerador es la derivada del denominador. Por tanto:
![]()
es decir,
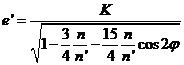
siendo K una constante.
Recordando (124.9) esta expresión de e![]() puede escribirse, elevando al cuadrado,
puede escribirse, elevando al cuadrado,
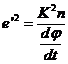
y como que según (119.9) y (123.9) es
![]()
es
![]()
con ![]() constante. Luego,
podemos escribir
constante. Luego,
podemos escribir
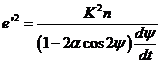
o sea
con
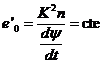
Desarrollando (126.9) obtenemos:
Siendo la excentricidad media e![]() 0 =
0.0549, la excentricidad e
0 =
0.0549, la excentricidad e![]() varía entre
varía entre
e![]() 0 (1- a) = 0.0448 y e
0 (1- a) = 0.0448 y e![]() 0 (1+ a) = 0.0650
0 (1+ a) = 0.0650
d) Ecuación del centro. Evección : De (122.9) y (127.9) deducimos que la órbita está definida por las dos relaciones siguientes:
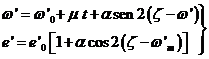 (128.9)
(128.9)
no siendo perturbado el eje mayor a’ (114.9).
Calculemos ahora la ecuación del centro de esta órbita deformable. Sea M’p la anomalía media perturbada de la Luna:
donde
![]()
o también
donde M’ es la parte secular de M’p:
![]()
De (130.9) deducimos:
![]() (131.9)
(131.9)
y llevando los
valores de e![]() y senM
y senM![]() p a la
expresión (129.9) obtenemos:
p a la
expresión (129.9) obtenemos:
![]()
de donde, despreciando los términos de segundo orden
![]()
El término ![]() senM
senM![]() representa la ecuación del centro en una órbita elíptica de
magnitud invariable (primer término del desarrollo de la ecuación del centro),
en la que la línea de los ápsides giraría uniformemente en sentido directo con
velocidad angular m. El término
representa la ecuación del centro en una órbita elíptica de
magnitud invariable (primer término del desarrollo de la ecuación del centro),
en la que la línea de los ápsides giraría uniformemente en sentido directo con
velocidad angular m. El término ![]() a sen(M
a sen(M![]() -2y) representa una desigualdad que se suma a la
ecuación del centro y que depende del seno del argumento M
-2y) representa una desigualdad que se suma a la
ecuación del centro y que depende del seno del argumento M![]() -2y; recibe
el nombre de evección y
su descubrimiento se atribuye a Ptolomeo. Teniendo en cuenta el significado de M
-2y; recibe
el nombre de evección y
su descubrimiento se atribuye a Ptolomeo. Teniendo en cuenta el significado de M![]() -2y vemos que el tiempo interviene en la ecuación bajo el factor
-2y vemos que el tiempo interviene en la ecuación bajo el factor
n![]() -2n +m = 40739
-2n +m = 40739![]() .42
.42
correspondiendo a un periodo de 31.81 días.
El coeficiente de la evección es
![]()
cuyo valor es de 57![]() .4.
.4.
La serie obtenida por Delaunay es
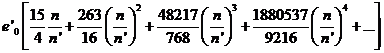
cuya suma es 1º 16![]() 26
26![]() .
.
La ecuación del centro es (recordar 4.7.1)
![]()
Obsérvese que los
coeficientes son grandes debido a qué la excentricidad ![]() es relativamente grande.
es relativamente grande.
e) Reduccíón a la eclíptica: No es propiamente una perturbación sinó una reducción, análoga a la reducción al ecuador (4.7.2), que fue introducida en la teoría de la Luna por Tycho Brahe y que expresa la diferencia entre la longitud celeste y la longitud sobre la órbita. Viene dada por
![]()
donde l es la longitud celeste, i![]() la inclinación de la órbita de la Luna sobre la eclíptica y h el argumento de latitud L - W.
la inclinación de la órbita de la Luna sobre la eclíptica y h el argumento de latitud L - W.
Resumimos a continuación los resultados obtenidos que afectan a la longitud:
|
|
aceleración secular |
|
|
ecuación del centro |
|
|
variación |
|
|
desigualdad paraláctica |
|
|
ecuación anual |
|
|
evección |
|
|
reducción a la eclíptica |
9.3.6 Desigualdades que dependen de
una perturbación ortogonal al
plano orbital de la Luna
Hasta ahora hemos supuesto la fuerza perturbatriz![]() sobre el plano de la órbita lunar; pero, en realidad está
situada en el plano que contiene los centros del Sol, de la Tierra y de la
Luna. Admite pues, además de las componentes S y P , una componente T perpendicular al plano de la órbita.
sobre el plano de la órbita lunar; pero, en realidad está
situada en el plano que contiene los centros del Sol, de la Tierra y de la
Luna. Admite pues, además de las componentes S y P , una componente T perpendicular al plano de la órbita.
En la expresión (60.9) de la fuerza
perturbatriz ![]() intervienen dos
términos el primero de los cuales representa un vector dirigido según el radio
vector de la Luna y el segundo un vector paralelo al radio vector Tierra-Sol.
Recordemos que, tomando el sentido positivo hacia el Sol, este último es
intervienen dos
términos el primero de los cuales representa un vector dirigido según el radio
vector de la Luna y el segundo un vector paralelo al radio vector Tierra-Sol.
Recordemos que, tomando el sentido positivo hacia el Sol, este último es
![]() (132.9)
(132.9)
y su módulo
Si limitamos el desarrollo (133.9) a su primer término y despreciamos las excentricidades este módulo es
![]()
(A![]() s, r’
s, r’![]() a’,
a’, ![]() ).
).
La proyección sobre la normal al plano de la órbita es la componente ortogonal buscada.
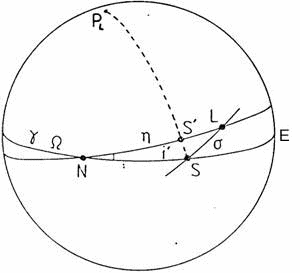
FIG. 12.9
Representemos sobre la esfera celeste la eclíptica E, la órbita de la Luna L, el Sol S, el nodo ascendente de la órbita de la Luna N y el polo norte PL del plano de la órbita de la Luna (Fig.12.9).
Pongamos
NL=h
y sean, por otra
parte, i![]() la inclinación de la órbita de la Luna sobre la eclíptica, W
la inclinación de la órbita de la Luna sobre la eclíptica, W![]() la longitud del nodo y s la
distancia SL. En primera aproximación
tendremos:
la longitud del nodo y s la
distancia SL. En primera aproximación
tendremos:
![]()
La componente ortogonal T tiene por expresión
![]()
(el signo menos indica que se proyecta hacia la parte negativa de la normal).
Ahora bien,
sen SS![]() = sen i
= sen i![]() sen NS = sen i
sen NS = sen i![]() sen ( h-s )
sen ( h-s )
luego,
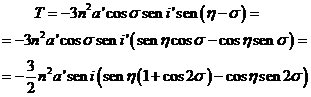
Es decir:
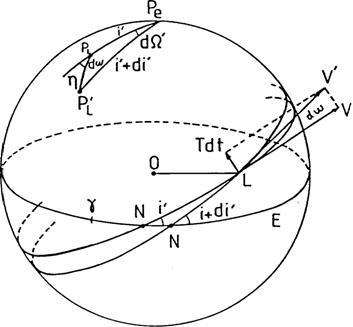 FIG. 13.9
FIG. 13.9
Veamos cuales son los efectos de una perturbación ortogonal
instantánea. Supongamos que la órbita de la Luna es circular. Sea ![]() la velocidad de la Luna en su órbita y
compongamos esta velocidad con
la velocidad de la Luna en su órbita y
compongamos esta velocidad con ![]() .La velocidad resultante, que representa la velocidad
perturbada
.La velocidad resultante, que representa la velocidad
perturbada ![]() continúa siendo
perpendicular al radio vector
continúa siendo
perpendicular al radio vector ![]() y forma con
y forma con ![]() un ángulo dw. La perturbación hace girar el plano de la órbita, alrededor de
un ángulo dw. La perturbación hace girar el plano de la órbita, alrededor de ![]() , un ángulo dw; el
nodo pasa de N a N
, un ángulo dw; el
nodo pasa de N a N![]() desplazándose dW
desplazándose dW![]() y la inclinación de la órbita varía en di
y la inclinación de la órbita varía en di![]() .
.
Por ser dw muy pequeño podemos escribir
donde Tdt y V son los módulos de ![]() y
y ![]() .
.
Por otra parte, sean PL
y PL![]() los polos de las órbitas lunares no perturbada y perturbada y Pe el polo de la eclíptica.
En el triángulo
los polos de las órbitas lunares no perturbada y perturbada y Pe el polo de la eclíptica.
En el triángulo ![]() se verifica:
se verifica:
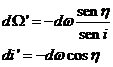 (136.9)
(136.9)
de donde
![]()
y teniendo en cuenta (135.9)
![]()
Sustituyendo T por su valor (134.9):
![]()
y desarrollando y operando el segundo miembro:
Análogamente, a partir de la segunda ecuación de (136.9) obtenemos:
![]()
o también, operando el segundo miembro:
Recordando el significado de los distintos argumentos, las ecuaciones diferenciales (137.9) y (138.9) se pueden escribir también en la forma:
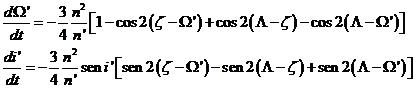 (139.9)
(139.9)
El periodo de los términos en ![]() es del orden de 6
meses y es el más largo. Los términos en
es del orden de 6
meses y es el más largo. Los términos en ![]() tienen un periodo
igual a la semirrevolucion sinódica y el de los términos en
tienen un periodo
igual a la semirrevolucion sinódica y el de los términos en ![]() es de una
semirrevolución draconítica.
es de una
semirrevolución draconítica.
Consideraremos sólo los términos de periodo largo y escribiremos:
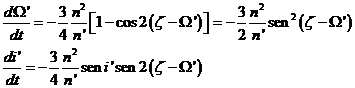 (140.9)
(140.9)
a) Movimiento
del nodo: La primera de las ecuaciones (140.9)
es del mismo tipo que la (116.9); por tanto, podemos utilizar
para integrarla el mismo procedimiento que utilizamos allí haciendo ahora ![]() . Hallaremos para la longitud del nodo:
. Hallaremos para la longitud del nodo:
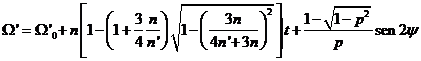 (141.9)
(141.9)
con
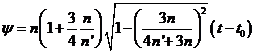 (142.9)
(142.9)
El movimiento medio sidéreo del nodo es, en primera aproximación
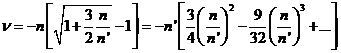 (143.9)
(143.9)
serie cuya suma es
-193![]() .8. El valor observado es de -190
.8. El valor observado es de -190![]() .77.
.77.
La serie obtenida por Delaunay es:
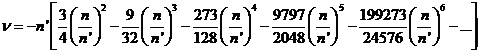
La longitud del nodo afectada de su principal desigualdad es
![]() (144.9)
(144.9)
donde W![]() m es la longitud media y
m es la longitud media y 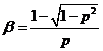 .
.
El periodo de esta desigualdad es de 173.31 días y su semiamplitud es, teniendo en cuenta el valor de p:
![]()
b) Desigualdades
de la inclinación: Para
estudiar las desigualdades de la inclinación partamos de la segunda ecuación de
(140.9) y del valor de dj/dt que se deduce de hacer ![]() . Tendremos
. Tendremos
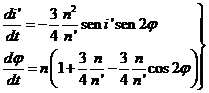 (145.9)
(145.9)
Eliminando dt entre estas dos ecuaciones resulta
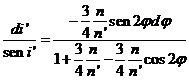
ecuación diferencial a variables separables que podemos resolver haciendo
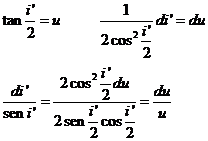
Es decir,
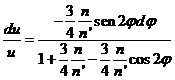
ecuación del mismo tipo que la (125.9) cuya integral es, una vez restablecido el valor de la variable,
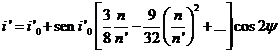
Vemos pues que la inclinación está afectada de una desigualdad del
mismo periodo que el nodo, 173.31 días, y su semiamplitud es b sen ![]() = 8
= 8![]() .2.
.2.
9.3.7 Desigualdades de la latitud
celeste de la Luna
Calcularemos la latitud celeste de la Luna mediante la ecuación
la cual contiene las desigualdades correspondientes a la longitud de la Luna y las desigualdades correspondientes al nodo y la inclinación.
Despreciemos las desigualdades de la inclinación y del nodo y pongamos
donde h crece uniformemente con el tiempo y ![]() representa las
desigualdades periódicas de la longitud de la Luna y se escribe
representa las
desigualdades periódicas de la longitud de la Luna y se escribe
siendo l una función lineal del tiempo y k una constante.
De (147.9) deducimos
![]()
y sustituyendo en (146.9), teniendo en cuenta (148.9) y operando, obtenemos:
![]() (149.9)
(149.9)
forma general del desarrollo del seno de la latitud supuesto fijo el plano de la órbita.
Las desigualdades de la latitud que se obtienen como consecuencia de las del nodo y de la inclinación son pequeñas a excepción de la que recibe el nombre
de gran desigualdad de la latitud . Si el plano de la órbita no sufre otra perturbación que la retrogradación del nodo, salvo desigualdades periódicas, la latitud toma el valor
Desarrollando en serie (146.9) y (150.9), tomando solamente los términos de primer orden en ![]() y restando obtenemos:
y restando obtenemos:
![]()
y sustituyendo las desigualdades por sus expresiones
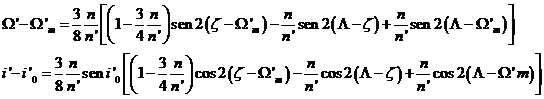
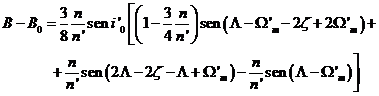 (151.9)
(151.9)
El tercer término de esta expresión
(151.9) contiene únicamente el argumento de latitud de
la Luna L-W’m
y puede englobarse en la inclinación siendo este valor corregido de ![]() el que se determina
por observación. Los otros dos términos de (151.9) son
términos semejantes y por tanto se pueden sumar. La parte secular de su
argumento es
el que se determina
por observación. Los otros dos términos de (151.9) son
términos semejantes y por tanto se pueden sumar. La parte secular de su
argumento es
![]()
Luego, el desarrollo de B es:
![]() (152.9)
(152.9)
Vemos pues que aparece una desigualdad de la latitud celeste cuya
amplitud es de 17![]() 38
38![]() .
.
Si se tiene en cuenta que L está afectada por la variación puede escribirse
![]()
valor que afecta al desarrollo de la latitud (152.9), obteniéndose la gran desigualdad de la latitud en la forma:
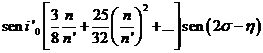
El tiempo interviene en su argumento con el coeficiente
![]()
que corresponde a
un periodo de 32.28 días. La amplitud de la gran desigualdad es de 21![]() 10
10![]() .
.