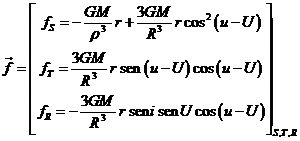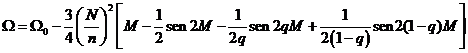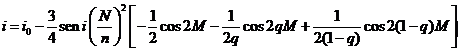8.7 Perturbaciones debidas a la acción de otro astro lejano
Partiremos de la fórmula
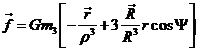 (62.8)
(62.8)
obtenida en
7.5.1, que expresa el valor de la fuerza perturbatriz por unidad de masa debida
a la presencia de un astro lejano (en aquel caso la Luna). En ella, m3 es
la masa de la Luna, ![]() es la distancia Tierra
- satélite artificial,
es la distancia Tierra
- satélite artificial, ![]() la distancia
satélite-Luna,
la distancia
satélite-Luna, ![]() la distancia
Tierra—Luna y ψ el ángulo que forman los vectores
la distancia
Tierra—Luna y ψ el ángulo que forman los vectores ![]() y
y ![]() .
.
Seguiremos suponiendo aquí, para fijar ideas, que el astro perturbador
es la Luna y definiremos los elementos cuyas variaciones queremos hallar
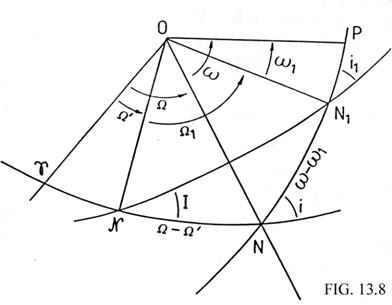
respecto al plano de la órbita de la Luna. Sean NN1 la órbita del
satélite, NN el ecuador y NN1 la órbita
lunar (Fig. 13.8). N es el nodo de la órbita
lunar, N el nodo de la órbita del satélite (los dos respecto al ecuador)
y N1 es el
nodo de la órbita del satélite respecto a la órbita lunar. Sean, además, I la
inclinación del plano de la órbita de la Luna con respecto al del ecuador; i,
la del plano de la órbita del satélite con respecto al mismo plano del ecuador,
e i1 la de la órbita del satélite con respecto al de la órbita de
la Luna. Llamemos, por otra parte, ![]() ,
, ![]() y
y ![]() a los argumentos de los nodos N,
N y N1 respectivamente, este último contado desde la línea de
los nodos ON, y
a los argumentos de los nodos N,
N y N1 respectivamente, este último contado desde la línea de
los nodos ON, y ![]() y
y ![]() , a los argumentos del periastro contados sobre la órbita del satélite
desde su intersección con el ecuador y la órbita lunar respectivamente.
, a los argumentos del periastro contados sobre la órbita del satélite
desde su intersección con el ecuador y la órbita lunar respectivamente.
El problema que tendremos que resolver es, pues, el de calcular ![]() , i1 y
, i1 y ![]() conocidos I,
conocidos I, ![]() ,
, ![]() , i y
, i y ![]() . Para ello podemos aplicar las fórmulas de la trigonometría esférica
al triángulo NNN1 (Fig. 13.8) en el que se
conocen dos ángulos (I, 180º - i) y un lado
. Para ello podemos aplicar las fórmulas de la trigonometría esférica
al triángulo NNN1 (Fig. 13.8) en el que se
conocen dos ángulos (I, 180º - i) y un lado ![]() . Una vez determinados estos elementos les seguiremos llamando, por
comodidad en los cálculos,
. Una vez determinados estos elementos les seguiremos llamando, por
comodidad en los cálculos, ![]() , i y
, i y ![]() , con el bien entendido de que los tenemos
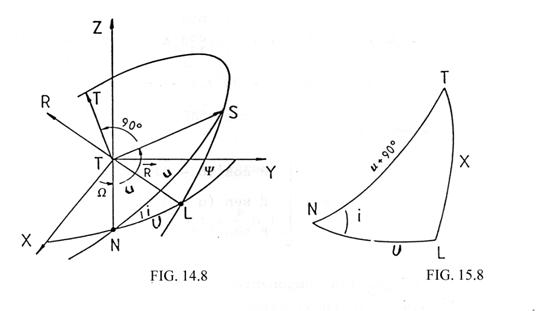
referidos al plano de la órbita lunar que tomaremos como plano fundamental XY (Fig. 14.8).
, con el bien entendido de que los tenemos
referidos al plano de la órbita lunar que tomaremos como plano fundamental XY (Fig. 14.8).
H
HHallaremos las componentes de ![]() en el sistema S,
T, R. Observemos que
en el sistema S,
T, R. Observemos que ![]() es suma de dos
vectores, el primero de los cuales sólo tiene componente según S. El
segundo está multiplicado por cos
es suma de dos
vectores, el primero de los cuales sólo tiene componente según S. El
segundo está multiplicado por cos ![]() , factor que podemos calcular a partir del triángulo N
L S (nodo – Luna - satélite) (Fig. 14.8):
, factor que podemos calcular a partir del triángulo N
L S (nodo – Luna - satélite) (Fig. 14.8):
![]()
fórmula
que podemos simplificar si suponemos que la órbita del satélite es de inclinación
pequeña ![]() . Escribiremos, pues:
. Escribiremos, pues:
![]() (63.8)
(63.8)
Por otra parte, si consideramos el triángulo TLN y llamamos ![]() al arco TL, podemos
escribir (Fig. 15.8):
al arco TL, podemos
escribir (Fig. 15.8):
![]()
y,
utilizando la misma hipótesis ![]() :
:
![]()
De todo ello resulta que los cosenos directores de ![]() con respecto al
sistema S,T,R son:
con respecto al
sistema S,T,R son:
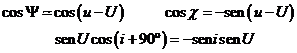
y por tanto,
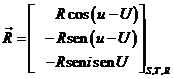
Luego, las componentes de ![]() , designando por M la masa de la Luna, serán:
, designando por M la masa de la Luna, serán:
Si el astro perturbador describiese una órbita circular alrededor de la Tierra, GM/R3 sería constante. Llamando N2 a dicha constante, (64.8) quedaría:
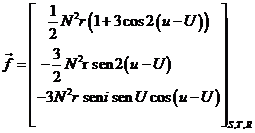 (65.8)
(65.8)
habiendo
supuesto ![]() .
.
Partiendo de la primera ecuación de Gauss tendremos:
![]()
Suponiendo
![]() e integrando según M,
para lo cual haremos
e integrando según M,
para lo cual haremos
![]()
tendremos:
y como que lo que nos interesa son las perturbaciones seculares, para integrar podemos tomar u = M, con lo cual (66.8) se escribirá, operando:
![]()
de donde
fórmula que nos dice que el nodo retrograda a lo largo del plano fundamental.
Si efectuáramos la integración entre 0 y M encontraríamos:
que expresa una oscilación del nodo que tiene lugar al mismo tiempo que la retrogradación.
Si aplicásemos las expresiones (67.8) y (68.8) al caso de la Luna perturbada por el Sol (n ![]() 13º/día, N
13º/día, N ![]() 1º/día), obtendríamos que el
nodo de la órbita lunar retrograda, dando una vuelta completa en 18,6 años,
mientras va oscilando alrededor de su posición media.
1º/día), obtendríamos que el
nodo de la órbita lunar retrograda, dando una vuelta completa en 18,6 años,
mientras va oscilando alrededor de su posición media.
Partiendo de la segunda fórmula de Gauss obtenemos
![]()
y, por consideraciones análogas al caso anterior,
![]() (69.8)
(69.8)
Utilizando la conocida fórmula trigonométrica
![]()
obtenemos:
![]()
y volviéndola a aplicar:
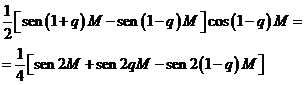
Por tanto:
![]() (70.8)
(70.8)
de donde
Si integrásemos entre 0 y M obtendríamos
De estas expresiones (71.8) y (72.8) se deduce que sólo hay perturbaciones periódicas.
Para estudiar las perturbaciones producidas sobre el semieje mayor de
la órbita, partiremos de la tercera fórmula de Gauss y, dado que suponemos e ![]() 0 se reducirá a
0 se reducirá a
![]()
es decir, en nuestro caso:
![]()
Luego, con c = na2:
![]()
es decir,
![]()
e integrando entre 0 y M:
![]()
o sea, que tampoco en este caso hay términos seculares.
Un cálculo análogo al efectuado nos daría
![]()
Para el estudio de las variaciones del argumento del perigeo, partiendo de la quinta fórmula de Gauss, haciendo en ella V = M y teniendo en cuenta la primera, obtenemos:
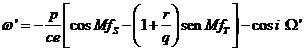
Sustituyendo ![]() y
y![]() por sus valores (65.8),
haciendo
por sus valores (65.8),
haciendo ![]() y
y ![]() , y utilizando relaciones trigonométricas análogas a las
utilizadas para calcular
, y utilizando relaciones trigonométricas análogas a las
utilizadas para calcular ![]() , integrando, obtenemos:
, integrando, obtenemos:
![]()
e integrando entre 0 y M:
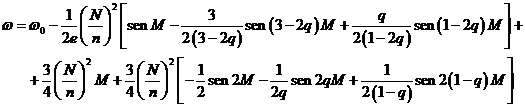
Hay un término secular, lo cual era de esperar porque también aparece
en ![]() , y los demás son términos periódicos.
, y los demás son términos periódicos.