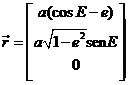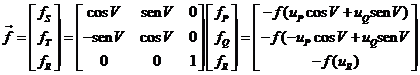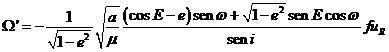8.6 Perturbaciones debidas a la
presión de radiación solar
Estudiaremos ahora las perturbaciones que sobre los elementos orbitales de un satélite artificial produce la presión de radiación solar directa, fenómeno que hay que tener en cuenta cuando se utilizan satélites con elevada superficie respecto a la masa. Despreciaremos la radiación reflejada procedente de los planetas (sobre todo de la Tierra) y de la Luna.
Se sabe que a una altitud de 800 km los efectos de la presión de radiación solar directa y la resistencia de la atmósfera sobre un satélite artificial de la Tierra son del mismo orden. Es más, para las temperaturas usuales exosféricas y por encima de los 800 km los efectos de la presión de radiación son mayores que los de la resistencia de la atmósfera para satélites que se mueven en órbitas circulares.
 Para un estudio más preciso de la evolución orbital y para satélites en
órbitas muy excéntricas, los dos efectos deberán ser considerados simultáneamente.
Para un estudio más preciso de la evolución orbital y para satélites en
órbitas muy excéntricas, los dos efectos deberán ser considerados simultáneamente.
Sea ![]() la fuerza por unidad de masa debida a la
presión de radiación solar directa. Llamemos
la fuerza por unidad de masa debida a la
presión de radiación solar directa. Llamemos ![]() al vector de posición
geocéntríco del Sol y
al vector de posición
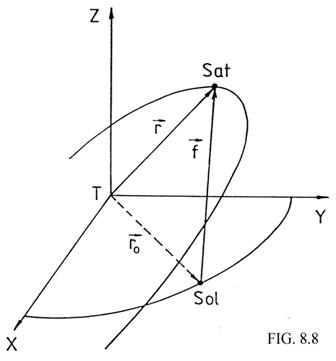
geocéntríco del Sol y ![]() al vector de posición geocéntrico del satélite. De la Fig. 8.8 se deduce que la fuerza perturbatriz
al vector de posición geocéntrico del satélite. De la Fig. 8.8 se deduce que la fuerza perturbatriz ![]() se podrá expresar de la forma
se podrá expresar de la forma
![]() (50.8)
(50.8)
y puesto que r es siempre mucho más pequeño que r0 se podrá escribir
con ![]() y
y ![]() (vector unitario
Tierra - Sol) siendo
(vector unitario
Tierra - Sol) siendo
donde k es un factor que depende del albedo y de la forma del satélite (k = 1 para una esfera perfectamente reflectante), s es la sección recta del satélite, m su masa y q0 se toma igual a 4.65x10-5 dinas suponiendo constante la distancia geocéntrica del Sol y la intensidad de la radiación solar a esta distancia.
El vector ![]() , unitario en la dirección del Sol, varía con la posición
relativa del Sol respecto a la Tierra; pero, en primera aproximación, podemos
suponer que durante una vuelta del satélite
, unitario en la dirección del Sol, varía con la posición
relativa del Sol respecto a la Tierra; pero, en primera aproximación, podemos
suponer que durante una vuelta del satélite ![]() se mantiene constante.
En efecto, en un día un satélite geodésico da ocho vueltas a la Tierra y el Sol
recorre aproximadamente 1º en su movimiento ánuo aparente alrededor de la
Tierra. Por tanto, en una vuelta del satélite, el Sol se habrá desplazado
sólamente 1/8 de grado y, en consecuencia, podemos despreciar el movimiento del
Sol. Luego, según (51.8) y (52.8)
se mantiene constante.
En efecto, en un día un satélite geodésico da ocho vueltas a la Tierra y el Sol
recorre aproximadamente 1º en su movimiento ánuo aparente alrededor de la
Tierra. Por tanto, en una vuelta del satélite, el Sol se habrá desplazado
sólamente 1/8 de grado y, en consecuencia, podemos despreciar el movimiento del
Sol. Luego, según (51.8) y (52.8) ![]() será una fuerza de módulo y dirección
constantes a lo largo de un periodo.
será una fuerza de módulo y dirección
constantes a lo largo de un periodo.
Resolveremos este caso en el sistema P,Q,R (3.11.3) y utilizaremos la fórmula
Las componentes de ![]() en el sistema P,Q,R
serán
en el sistema P,Q,R
serán
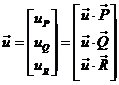 (54.8)
(54.8)
y, por
consiguiente, las de ![]() :
:
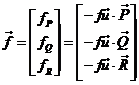 (55.8)
(55.8)
 Al aplicar la fórmula (53.8) tendremos en cuenta
que responde al caso en que el satélite permanece siempre iluminado; pero, si el
satélite penetra en el cono de sombra de la Tierra, mientras permanece
eclipsado la presión de radiación no actúa sobre él y, por consiguiente, su
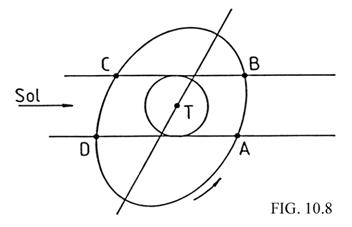
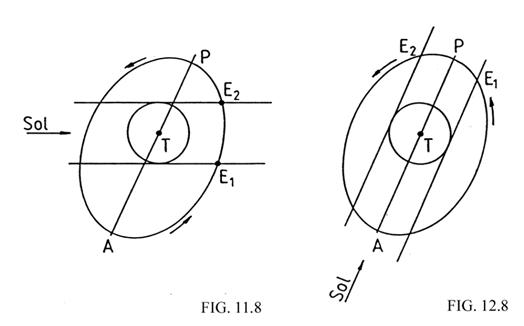
movimiento no se ve perturbado por esta causa. Es preciso pues calcular cuando
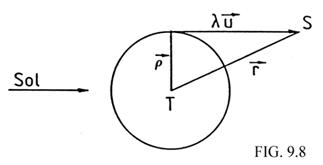
se producirá un eclipse. Como que la distancia del satélite a la Tierra es
mucho más pequeña que su distancia al Sol, podemos suponer que la Tierra
proyecta un cilindro de sombra en lugar de un cono (Fig. 9.8).
Llamando
Al aplicar la fórmula (53.8) tendremos en cuenta
que responde al caso en que el satélite permanece siempre iluminado; pero, si el
satélite penetra en el cono de sombra de la Tierra, mientras permanece
eclipsado la presión de radiación no actúa sobre él y, por consiguiente, su
movimiento no se ve perturbado por esta causa. Es preciso pues calcular cuando
se producirá un eclipse. Como que la distancia del satélite a la Tierra es
mucho más pequeña que su distancia al Sol, podemos suponer que la Tierra
proyecta un cilindro de sombra en lugar de un cono (Fig. 9.8).
Llamando ![]() al radio
de la Tierra, en el instante de entrada o salida del satélite del cilindro de
sombra tendremos:
al radio
de la Tierra, en el instante de entrada o salida del satélite del cilindro de
sombra tendremos:
![]()
y como que ![]() y
y ![]() son perpendiculares:
son perpendiculares:
![]()
o sea:
![]()
Por otra parte, el módulo de ![]() es
es ![]() y, por tanto:
y, por tanto: