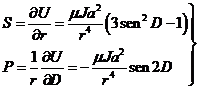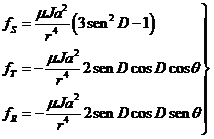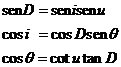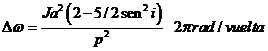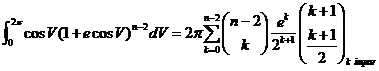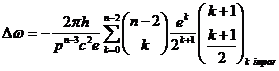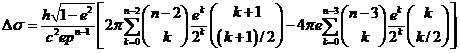8.4 Perturbaciones debidas al potencial terrestre

Recordemos la expresión del potencial terrestre obtenida en 2.3.2, fórmula (31.2):

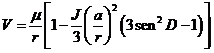(19.8)

(20.8)

es el potencial no newtoniano.

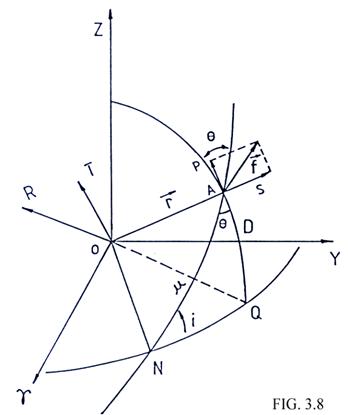
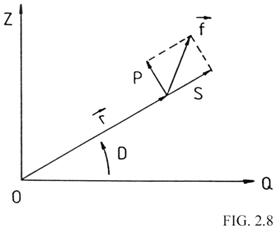Sean S y P las componentes radial y perpendicular, respectivamente, de la fuerza perturbatriz correspondiente al potencial terrestre (Fig. 2.8), iguales a las componentes del gradiente de U:

(21.8)

Nos interesa ahora hallar las componentes f_S, f_T, f_R de la fuerza perturbatriz para sustituirlas en las ecuaciones de Gauss. De la figura 3.8 deducimos:

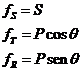
y sustituyendo en (21.8) tendremos

(22.8)

Por otro lado deducimos del triángulo NAQ de la figura 3.8 las relaciones:

(23.8)

Que sustituidas en (22.8) nos dan

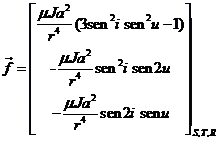
Escribiendo la expresión de la variación de los elementos en función de la anomalía verdadera teniendo en cuenta el valor , obtenemos:

(24.8)

Sustituiremos sucesivamente por los valores de las variaciones de los elementos orbitales dadas por las fórmulas de Gauss. En primer lugar, para tendremos, recordando (I):

y resolviendo la integral (se sugiere utilizar el método de resolución que nos da la teoría de residuos) se obtiene:

(25.8)

fórmula que nos da la variación de en una vuelta.

Si i< 90º (movimiento directo), , el nodo retrograda.

Si i = 90º (órbita polar),

Si i >90º (movimiento retrógrado), , el nodo avanza.

Para hallar la variación de la inclinación partiremos de la segunda ecuación de Gauss, fórmula (II) y sustituiremos en (24.8) por i’. Tendremos:

que una vez integrado nos dará:

lo cual nos dice que la fuerza perturbatriz debida al potencial terrestre no afecta la inclinación de la órbita.

El mismo resultado se halla para las variaciones del semieje mayor y de la excentricidad. Es decir, se obtiene

La quinta ecuación de Gauss nos dará la variación del argumento del periastro. En efecto, sustituyendo (V) en (24.8) e integrando, obtendremos:

Si , es . El ángulo i es entonces de i_c = (tan i = 2). Dicha inclinación, que recibe el nombre de inclinación crítica, es aquella con que debe lanzarse un satélite artificial para que la forma de la Tierra no influya en el argumento del periastro. De hecho, con esta inclinación fueron lanzados los primeros satélites rusos.

Si i = i_c no hay avance del periastro

Si i < i_c el periastro avanza

Si i > i_c el periastro retrograda.

Finalmente la sexta ecuación de Gauss nos proporcionará la variación de M o lo que es equivalente de . Sustituyendo (VI) en (24.8) y operando se obtiene:

Si  sen² i = 2/3,  σ  no  varía.  Entonces    y  tan² ic = 2.

Si i < 54º44 es Ds > 0

Si i = i_c es Ds = 0

Si i > 54º44 es Ds < 0

i_c es la inclinación con que se lanzaron los Explorer.

8.4.1 Perturbaciones debidas al potencial terrestre en el caso particular de un potencial terrestre central

Estudiemos el caso en que la fuerza perturbatriz es de la forma

Es evidente que en el sistema S,T,R sólo tiene componente no nula en la dirección de S, es decir

Trabajaremos con la anomalía verdadera; por tanto, utilizaremos, igual que en el apartado anterior la fórmula (24.8).

Como que según (I) y (II), e i’ son proporcionales a f_R, serán

Para tendremos, recordando (III):

y siendo

resulta

Para , tendremos asimismo, haciendo uso de (IV):

resultando

Vemos pues que una fuerza perturbatriz central no afecta la posición del nodo ni la inclinación y tampoco la forma de la órbita.

En cambio, veremos que sí afecta el argumento del nodo y la época de paso por el periastro. En efecto, sustituyendo en primer lugar w en (24.8) tendremos:

El valor de la integral es

y por tanto:

Otra forma frecuente de expresar este resultado se obtiene con el cambio que da:

Sustituyendo ahora en (24.8) obtenemos:

y después del cálculo de la integral:

donde el primer sumatorio se extiende para valores impares de k y el segundo para valores pares.

ANTERIOR

ÍNDICE

SIGUIENTE