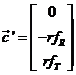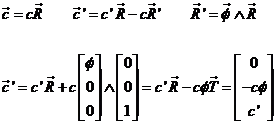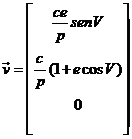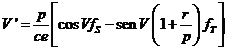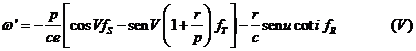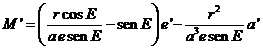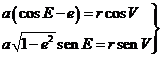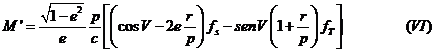8.2
Ecuaciones de Gauss
Deduciremos las ecuaciones de Gauss
a partir de las integrales del movimiento.
Sean, en el sistema S,T,R:
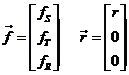
En el caso kepleriano, la ley de las
áreas toma la forma 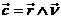 . En nuestro caso,
. En nuestro caso, 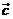 no es constante. Su
variación será:
no es constante. Su
variación será:
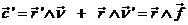
por tanto:
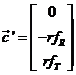 (9.8)
(9.8)
Por otra
parte:
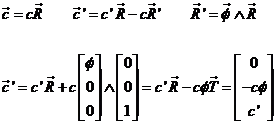 (10.8)
(10.8)
e
identificando (9.8) y (10.8)
resulta:
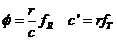 (11.8)
(11.8)
o sea,
teniendo en cuenta (8.8):
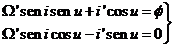 (12.8)
(12.8)
Multiplicando la primera de (12.8) por sen u y la segunda por cos u, sumando y
sustituyendo por la primera de las (11.8), obtenemos:
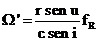 (I)
(I)
Multiplicando ahora la primera de (12.8) por cos u y la segunda por sen u, restando y
sustituyendo luego por la primera de las (11.8):
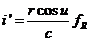 (II)
(II)
Si la fuerza perturbatriz no tiene tercera componente, es decir, si f
está en el plano de la órbita, según (I) y (II) no variarán ni el nodo ni la
inclinación de la órbita.
Para hallar la variación de 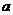 partiremos de la
integral de la energía:
partiremos de la
integral de la energía:
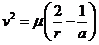
derivando:
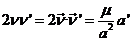
de donde:
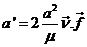 (13.8)
(13.8)
y recordando
que las componentes de 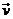 en el sistema S,T,R
son (ver 28.3):
en el sistema S,T,R
son (ver 28.3):
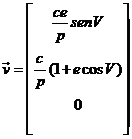
y además
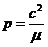
sustituyendo
en (13.8) y operando resulta:
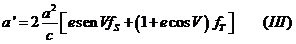
Partiendo de 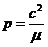 y derivando:
y derivando: 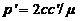 y teniendo en cuenta que
y teniendo en cuenta que 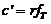 , sustituyendo:
, sustituyendo:
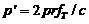 (14.8)
(14.8)
Despejando
ahora e2 de p = a(1 – e2) y derivando,
obtenemos:
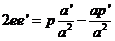
y
sustituyendo a’ por (III) y p’ por (14.8), despejando después e’ se obtiene:
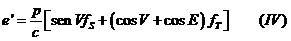
Se puede calcular la variación del elemento orbital 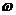 derivando
derivando 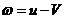 :
:
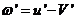
De la
tercera de (8.8) y (I) se obtiene
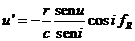 (15.8)
(15.8)
y de derivar
la expresión que nos da el radio vector 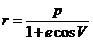 teniendo en cuenta los valores
de e’ y p’ ya obtenidos,
se halla
teniendo en cuenta los valores
de e’ y p’ ya obtenidos,
se halla
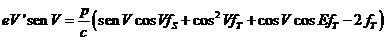
y poniendo
cos E en función de cos V, utilizando
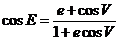
operando, agrupando
términos y simplificando se obtiene
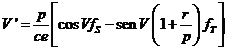 (16.8)
(16.8)
Sustituyendo (15.8) y (16.8)
en 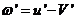 se obtiene finalmente:
se obtiene finalmente:
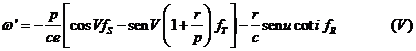
De 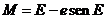 derivando, obtenemos
derivando, obtenemos
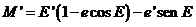 (17.8)
(17.8)
y de 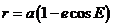 también derivando,
también derivando,
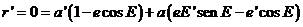
y
despejando E’:
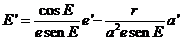
y
sustituyendo en (17.8):
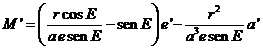
El
coeficiente de e’ es
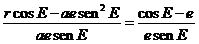
que se puede
expresar en función de V recordando que
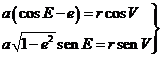
resultando
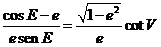
y
sustituyendo en M’
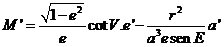
y
sustituyendo 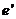 por (IV)
y
por (IV)
y 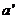 por (III),
agrupando términos y simplificando, obtendremos finalmente:
por (III),
agrupando términos y simplificando, obtendremos finalmente:
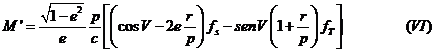
Las seis fórmulas indicadas por números romanos (del I al VI)
constituyen las llamadas fórmulas de Gauss y dan la variación de los
elementos orbitales al variar en un instante dado la velocidad del secundario a
causa de la fuerza perturbatriz que actúa sobre él. Las aplicaremos al estudio
del movimiento de satélites artificiales.
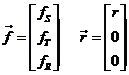
![]() . En nuestro caso,
. En nuestro caso, ![]() no es constante. Su
variación será:
no es constante. Su
variación será:![]()