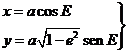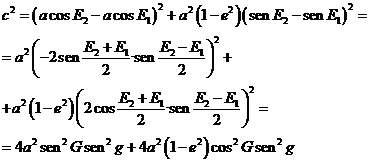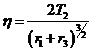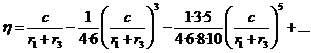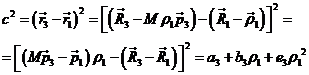6.4 Método de Olbers
En 1797 Olbers publicó un trabajo que tituló “Un ensayo sobre el método más
fácil y más conveniente de calcular la órbita de un cometa”. En el transcurso del
tiempo se han introducido algunos cambios en el método de Olbers que no afectan
a su concepto básico, quedando plenamente justificado el título con el que lo
presentó el autor.
Partiendo de tres posiciones de un cuerpo en su órbita, Olbers supone, tal
como había hecho Newton, que la cuerda que une las primera y tercera posiciones
queda dividida por el radio vector correspondiente a la segunda posición en dos
partes que son proporcionales a los intervalos de tiempo entre las observaciones
y obtiene una ecuación que liga las distancias geocéntricas de las primera y
tercera observación. Otra relación entre ellas la obtiene de la Ecuación de
Euler. Una vez halladas las distancias del cuerpo a la Tierra, el cálculo de
los elementos orbitales no presenta ninguna dificultad.
6.4.1
Teorema de Lambert para el movimiento elíptico
Sean E1 y E2 las
anomalías excéntricas de dos posiciones P1
y P2 en una órbita
elíptica de modo que E2 >
E1 (Fig. 7.6).
Llamemos:
![]()
y
![]()
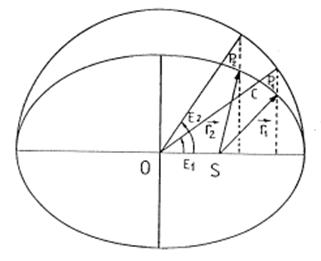
FIG.7.6
Si ![]() y
y ![]() son los
radios vectores heliocéntricos de Pl
y P2, teniendo en cuenta
que
son los
radios vectores heliocéntricos de Pl
y P2, teniendo en cuenta
que
![]()
y
![]()
se verificará:
![]()
Sea c la longitud de la cuerda
que una P1 con P2. Recordando que si tomamos
como ejes de referencia los ejes de la elipse, las coordenadas de un punto de
la misma son:
obtendremos para
el cuadrado de la distancia entre los puntos P1(x1,y1) y P2(x2,y2)
![]()
es decir,
aplicando (77.6)
y haciendo:
resulta, agrupando términos en (78.6):
![]()
y
También con este mismo cambio (79.6), es:
Hagamos ahora:
![]()
sumando y restando (81.6) y (80.6),
obtenemos:
Si t es
el tiempo que emplea el cuerpo
para pasar de la posición P1
a la P2, t = t2 - t1, en
virtud de la ecuación de Kepler tendremos:
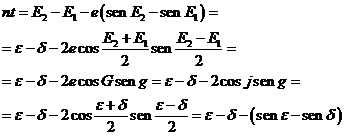
La relación
se conoce con el nombre de teorema de Lambert y ha sido deducida
para el movimiento elíptico.
e y d vienen dadas en función de r1 + r2, c
y a por las fórmulas (82.6) y (83.6); pero, no están
definidas unívocamente. Se demuestra (Plummer, 1960; p.51) que para un arco
pequeño basta tomar el menor valor positivo que satisface las ecuaciones (82.6) y (83.6).
Si el movimiento fuera parabólico, al
aplicar (81.6) con ![]() , teniendo en cuenta que el primer miembro es finito, el
factor
, teniendo en cuenta que el primer miembro es finito, el
factor ![]() debería tender a cero,
o lo que es lo mismo, el producto
debería tender a cero,
o lo que es lo mismo, el producto ![]() tender a 1. Pero, si
tender a 1. Pero, si ![]() , como que los cosenos están comprendidos entre -1 y +1, los
dos factores han de tender a 1. Luego, tanto g como j son ángulos muy
pequeños y por consiguiente e y d también
serían muy pequeños.
, como que los cosenos están comprendidos entre -1 y +1, los
dos factores han de tender a 1. Luego, tanto g como j son ángulos muy
pequeños y por consiguiente e y d también
serían muy pequeños.
Entonces, en virtud de (82.6)
y (83.6) tendríamos:
donde ![]() ,
, ![]() y
y ![]() .
.
Ahora bien, si en (84.6)
reemplazamos n por ![]() y desarrollamos en
serie
y desarrollamos en
serie ![]() y
y ![]() , obtendremos:
, obtendremos:
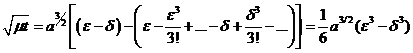 (87.6)
(87.6)
y si tenemos en cuenta (85.6) y (86.6),
podemos escribir la expresión:
que recibe el nombre de fórmula de
Euler y en la que se toma el signo menos si ![]() y el signo más si
y el signo más si ![]() .
.
La fórmula de Euler se puede aplicar al
estudio del movimiento de cometas; pero, si es ![]() , puede ocurrir que c
no quede bien determinada. En este caso se recurre a una sencilla modificación.
, puede ocurrir que c
no quede bien determinada. En este caso se recurre a una sencilla modificación.
Supongamos tres posiciones P1, P2, P3,
del cometa en su órbita parabólica y sean V1,
V2, V3 las
respectivas anomalías verdaderas.
Si ![]() podremos escribir (88.6) en la forma
podremos escribir (88.6) en la forma
donde c es ahora la longitud de la cuerda que une
las posiciones P1 y
P3.
Despejaremos c de esta ecuación. Para ello, sacando
factor común ![]() , tendremos:
, tendremos:
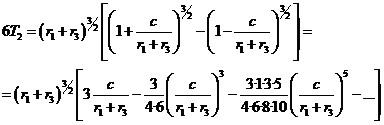
y haciendo
resultará
A partir de (91.6)
podremos hallar el desarrollo de ![]() en potencias impares
de h. En efecto, supongamos:
en potencias impares
de h. En efecto, supongamos:
![]()
y sustituyamos en (90.6). Será:
![]()
de donde, identificando, encontramos los coeficientes a3, a5,
… y el desarrollo de ![]() resulta ser:
resulta ser:
![]()
o también
donde
![]()
El valor de g se halla tabulado en función de h . Algunas veces se da directamente el
valor de gh en función de h. Otra posibilidad de hallar c es resolver directamente la ecuación (89.6).
Consideremos de nuevo el triángulo
determinado por el Sol, la Tierra y el cometa (Fig. 1.6).
La órbita se supone plana (movimiento no perturbado) y por consiguiente los
vectores de posición heliocéntricos son coplanarios. Se verifica, por tanto:
![]()
Dividamos por -c2 y llamemos ![]() al vector que
obtengamos:
al vector que
obtengamos:
Sea ![]() un vector coplanario
con
un vector coplanario
con ![]() y
y ![]() . Multipliquemos (93.6) escalarmente
por
. Multipliquemos (93.6) escalarmente
por ![]() . Tendremos:
. Tendremos:
![]()
es decir:
![]()
de donde
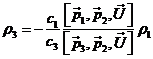
o también,
llamando
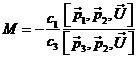
es
Por otra parte,
y
Si suponemos ![]() conocido, es conocido M ya que, según Olbers, el factor
conocido, es conocido M ya que, según Olbers, el factor ![]() es igual al
cociente entre el tiempo transcurrido entre la segunda y tercera observaciones
y el transcurrido entre la primera y la segunda y que
es igual al
cociente entre el tiempo transcurrido entre la segunda y tercera observaciones
y el transcurrido entre la primera y la segunda y que ![]() ,
, ![]() ,
, ![]() son datos
de observación y en (95.6), (96.6)
y (97.6) se conocen todos los coeficientes.
son datos
de observación y en (95.6), (96.6)
y (97.6) se conocen todos los coeficientes.
Supongamos que tenemos un primer valor de ![]() experimental. Podemos
calcular
experimental. Podemos
calcular ![]() ,
, ![]() y c. Por otra parte, podemos calcular h de (90.6) y hallar c con la fórmula (92.6).
Los dos valores de c obtenidos por
uno y otro método no concuerdan demasiado, dependiendo su diferencia del valor
inicial de
y c. Por otra parte, podemos calcular h de (90.6) y hallar c con la fórmula (92.6).
Los dos valores de c obtenidos por
uno y otro método no concuerdan demasiado, dependiendo su diferencia del valor
inicial de ![]() .
.
Variando ![]() podemos construir una
tabla de diferencias
podemos construir una
tabla de diferencias ![]() como función de
como función de ![]() . Buscaremos por interpolación cual es el valor que hace
. Buscaremos por interpolación cual es el valor que hace ![]() Una vez obtenido un
valor fiable de
Una vez obtenido un
valor fiable de ![]() hallaremos
hallaremos ![]() y
y ![]() y
y ![]() con la fórmulas (94.6), (95.6) y (96.6).
con la fórmulas (94.6), (95.6) y (96.6).
6.4.4 Cálculo
de los elementos orbitales
Recordemos las fórmulas del movimiento
parabólico (3.9).
Podemos escribir
![]()
donde q vendrá dado por
![]()
siendo c la constante de las áreas. Por
consiguiente:
![]()
siendo
![]()
y
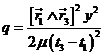
Si hacemos
![]()
las componentes heliocéntricas x, h de una posición cualquiera son
![]()
y la ecuación que
rige el movimiento parabólico
![]()
nos proporciona T. (Recordar una vez más las fórmulas (60.6) y (62.6)).