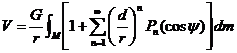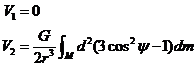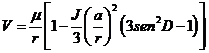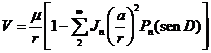2.3 Potencial terrestre
2.3.1 Expresión del campo gravitacional
terrestre bajo la forma de un desarrollo en polinomios de Legendre
Sea
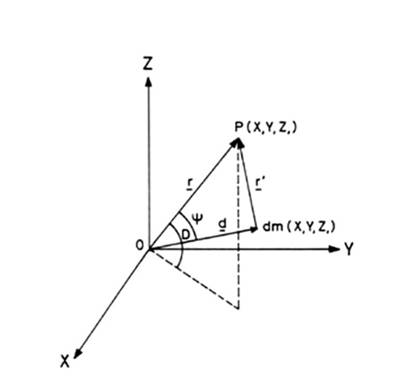
P un punto de la superficie de la
Tierra o exterior a ella, sometido a la atracción de la partícula de masa dm situada en el interior de la Tierra.
Sea O, centro de gravedad de la
Tierra (la cual suponemos de momento de forma cualquiera y de masa M) el origen de un sistema de
coordenadas cartesianas rectangulares X,
Y, Z; 
el vector de
posición de dm y 
el vector de
posición de P, con respecto a O; sea además 
el vector con
origen en el elemento de masa dm y
extremo en el punto P y 
el ángulo que forman
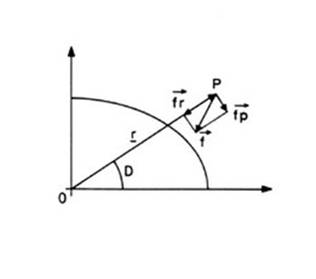
los vectores y (Fig. 9.2). El potencial en el punto P debido a dicha masa es:
FIG 9.2
(25.2)
donde G es la constante de
la gravitación universal y
con
Se tiene, sustituyendo en
(25.2):
(26.2)
La expresión entre
paréntesis puede ser desarrollada en serie convergente de polinomios en , llamados polinomios
de Legendre [1].
polinomios cuya expresión
general es:
siendo los primeros:
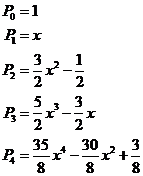
El
potencial V debido a la masa total M de la Tierra será, pues:
(27.2)
Integraremos
el segundo miembro de (27.2), para lo cual procederemos
término a término:
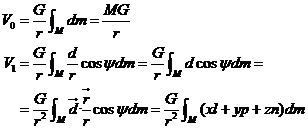
siendo (l, p, n) las
componentes del vector 
y (x,y,z) las del vector .
Pero,
si el origen del sistema de referencia está situado en el centro de masas de la
Tierra, es:
y por tanto,
(28.2)
Para
obtener esta nueva integral, teniendo en cuenta que 
, hagamos:
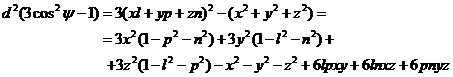
Sustituyendo
en (28.2) tendremos:
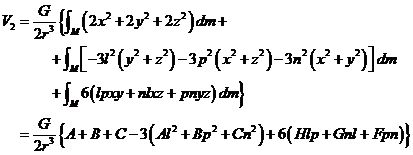
habiéndose tenido en
cuenta, para integrar, las relaciones que nos dan los momentos de inercia con
relación a los ejes coordenados:
y los momentos centrífugos
con relación a los planos coordenados:
siendo el tensor de inercia:
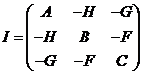
Sustituyendo
en (27.2) tendremos:
es decir, teniendo en
cuenta que la traza del tensor de inercia es:
y que
resultará
o también:
(29.2)
Si
la Tierra presentase una distribución esférica de masas, sería:
y entonces:
y por tanto
Si
como caso particular tomamos como ejes coordenados X,Y,Z los principales de inercia de la Tierra con respecto a su
centro de gravedad, los momentos centrífugos F, G, H son nulos y sólo quedan los momentos principales A,B,C. Si además suponemos que la
distribución de masas de la Tierra es de revolución alrededor del tercer eje
principal de inercia (eje Z), los
momentos principales de inercia serán iguales (A=B) y entonces I
adoptará la forma
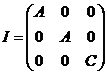
con lo que
y el potencial será:
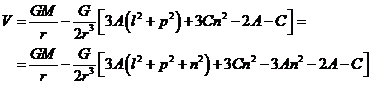
y recordando que :
(30.2)
Para
astros suficientemente alejados podemos suponer que el ecuador terrestre es el
plano determinado por los dos ejes principales iguales X,Y. Entonces, el ángulo
formado por la recta que une el centro de masas O con el punto P(X,Y,Z) y
el ecuador es la declinación D de P, siendo
Haciendo
además
donde a representa el
radio ecuatorial de la Tierra, y sustituyendo en (30.2),
tenemos:
(31.2)
Si
hubiésemos considerado más términos de la serie (27.2), hubiésemos obtenido
(32.2)
donde Pn
son los polinomios de Legendre y Jn son los armónicos o momentos de orden n de la
Tierra.
Comparando
la fórmula (31.2) y la (32.2)
escrita para n=2, deducimos que J2=2/3J , es decir:
J2
recibe el nombre de factor de la forma
dinámica de la Tierra y es una de las constantes primarias de la Astronomía
y Geodesia. Su valor actual (sistema de constantes IAU (1976)) es:
J2 = 0,00108263
Los armónicos J3 y J4 son negativos y del orden de ‑2.10-6.
El primer armónico que denota la “forma de pera" de la Tierra es el J3, lo cual es debido a que P3 es impar en sen D y, por tanto, en D. Dicha forma implica que el plano ecuatorial no sea de simetría
del potencial.
2.3.3 Aceleración j de la gravitación
De
la expresión (31.2) podemos deducir las componentes de
la aceleración total J:
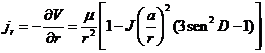(33.2)
Si
la Tierra presentase una distribución esférica de densidades sería J = 0 y
FIG 10.2
Pero, J es distinto de cero,
y en un punto simétrico, con declinación ‑D,
la aceleración radial jr
es la misma y la aceleración perpendicular jp
varía de signo pues en ella figura el sen 2D.
En cambio, si la declinación es complementaria la componente perpendicular es
la misma:
A igualdad de distancia r, la componente perpendicular de la
aceleración es máxima a los 45°. Por otra parte jp se anula en el ecuador y en los polos.
Si
tenemos en cuenta (29.2):
(34.2)
El primer término es
central. El tensor I aplicado al
vector 
de componentes (X,Y,Z)
es:
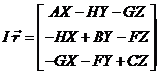
[1]
si desarrollamos por la fórmula del binomio de Newton 
los coeficientes de hn son los polinomios 
.